정의역의 모든 원소가 공역의 하나씩 빠짐없이 대응되면서 치역과 정의역의 관계 즉 임의의 실수를 대응시키면 무리식으로 된 관계에 있는 함수를 무리함수라 합니다. 여기서 주의할 점은 근호가 있는 수는 무리식이라하며 제곱근으로 근호 안이 0보다 큰 실수여야 합니다. 왜? 음수의 제곱근은 존재하지 않습니다. 어떤 수를 제곱하면 우리는 0이거나 양수가 된다는 것을 알고 있답니다. 결국 무리함수는 정의역이 근호안의 수는 0보다 크거나 같아야 합니다. 결국 정의역의 수를 대응 시키면 치역은 서서히 증가하는 것을 알 수 있습니다. 수의 감각을 좀 느켜보면 좋을 듯합니다.






시작점(0,0)인 무리함수는 4가지 모양을 하고 있습니다.
시작점(0,0)에서 오른쪽으로 서서히 증가하는 모양을 기준으로 설명을 합니다.
빨강색그래프를 y축 대칭이동하면 보라색그래프가 됩니다.
즉 시작점(0,0)에서 왼쪽으로 서서히 증가하는 모양임을 알 수 있죠.
빨강색그래프를 x축 대칭이동하면 노랑색그래프가 됩니다.
즉 시작점(0,0)에서 오른쪽 아래로 서서히 감소하는 모양임을 알 수 있죠.
빨강색그래프를 원점 대칭이동하면 파랑색그래프가 됩니다.
즉 시작점(0,0)에서 왼쪽 아래로 감소하는 모양임을 알 수 있죠.



가장 기본적인 무리함수는
시작점이 원점이고 x의 부호가 양수 y의 부호도 양수인 서서히 증가하는 1사분면에 그려집니다.
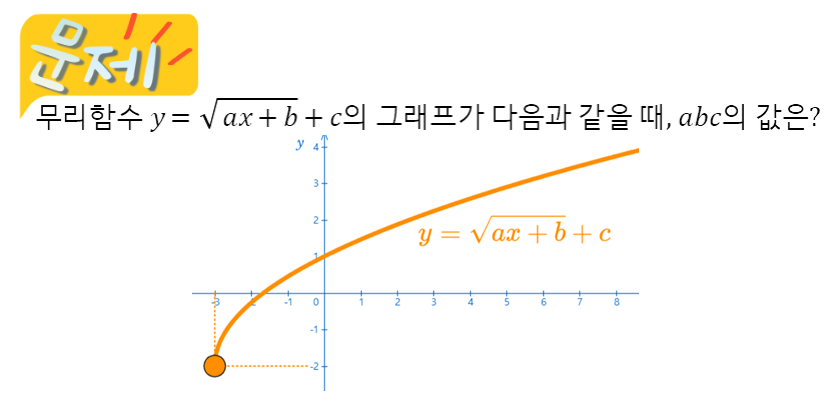
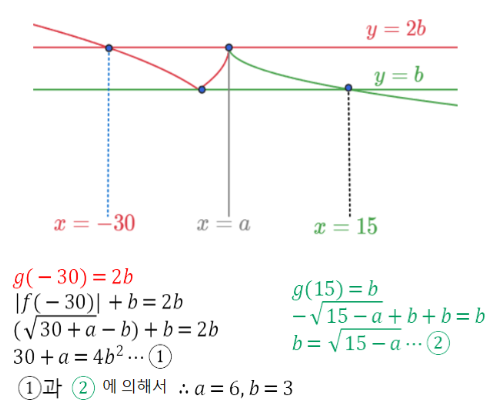
무리함수는 시작점을 발견하면 정의역과 치역의 범위를 알 수 있습니다.
시작점을 찾고 모양을 살펴봅니다.
시작점이 원점이고 그래프 모양이 1사분면, 2사분면, 3사분면, 4사분면 형태로 나타납니다.
무리함수그래프 그리는 방법은 시작점을 찾는다.
시작점을 찍는다.
x와 y의 부호를 살핀다.
부호가 변화가 없다면 1사분면에 그려지는 모양을 그린다.
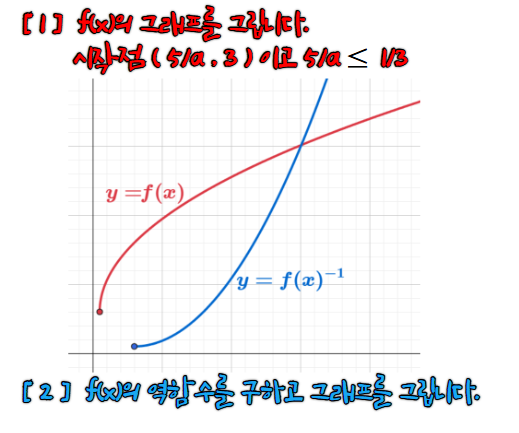
무리함수는 일대일대응입니다.
일대일대응이면 역함수가 존재합니다.
그리고 무리함수로 원앙새를 그려지는 ai그림입니다. 수학은 정말 아름답다는 것을 실감합니다. 질서가 곧 미다!!!!












'빨간머리앤 수학' 카테고리의 다른 글
| 로그의 재해석(1) (0) | 2025.01.15 |
|---|---|
| 거듭제곱근(1) 재 해석 (0) | 2025.01.06 |
| 순열 조합 재 해석 (52) | 2024.11.30 |
| 유리함수 개념의 재 해석(4) (0) | 2024.11.19 |
| 역함수 개념 재 해석(3) (1) | 2024.11.16 |




