대응에서 함수, 일대일함수, 일대일대응, 상수함수, 항등함수를 정의했습니다.
대응에서 함수가 되려면 정의역의 원소들이 어떻게 하나도 빠짐없이 공역에 대응하고 있는지만 살펴보면 됩니다.
일대일함수는 함수 중에서 정의역의 임의의 서로다른 두 원소의 대응시키면 함숫값이 서로 다른 경우를 말합니다.
일대일대응은 일대일함수이면서 치역과 공역이 같아야합니다.
상수함수는 함수 중에서 치역이 하나인 경우일 때이고
항등함수는 함수 중에서 자기자신으로의 대응시키는 것을 말합니다.
함수 중에서 일대일대응인 경우
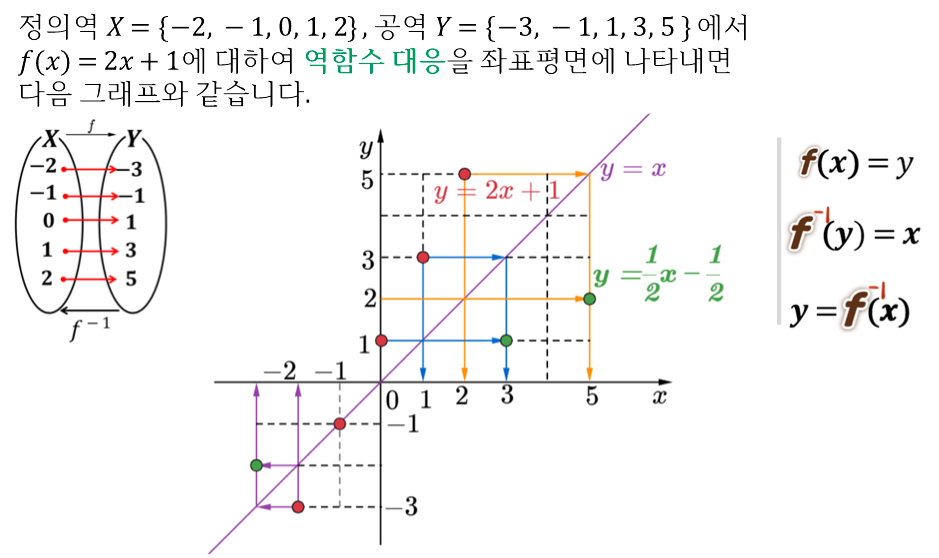
정의역이 공역이 되고 공역이 정의역이 되어 대응시킬 수 있게 됩니다.
이를 역함수라 부릅니다.
역함수는 함수와 구별하기 위해 기호 에프인버~ㄹ스로 읽습니다.

다음 함수그림을 단순화한 화살표로 표현한 것을 보고 등식으로 나타낼 수 있어야 합니다.

다음 함수 그림을 보고 일대일대응인 함수 f 는 역함수가 존재하는 것을 확인할 수 있습니다.
함수 g는 일대일대응이 아님을 알 수 있습니다.
함수 g를 공역에서 정의역으로의 대응을 살펴보면
천안은 2개가 대응되었고 보령은 대응할 수 없으니 함수가 만들어지지 않습니다. 그
래서 역함수 존재하지않는다고 말합니다.







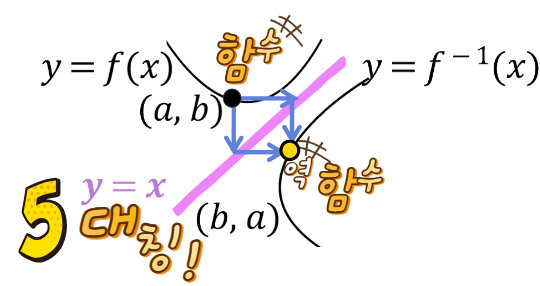

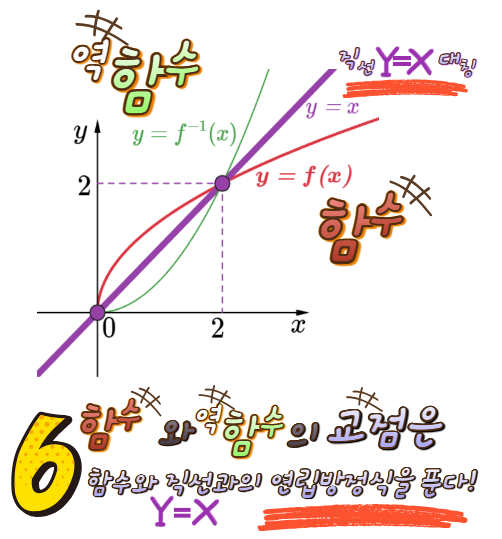


함수 중에서 일대일대응이면 역함수가 존재한다는 사실을 확인할 수 있었고 역함수의 성질 6개를 꼭 기억하여 문제에 적용할 수 있도록 노력해 보세요.





'빨간머리앤 수학' 카테고리의 다른 글
| 로그의 재해석(1) (0) | 2025.01.15 |
|---|---|
| 거듭제곱근(1) 재 해석 (0) | 2025.01.06 |
| 순열 조합 재 해석 (52) | 2024.11.30 |
| 무리함수 재해석 (4) | 2024.11.30 |
| 유리함수 개념의 재 해석(4) (0) | 2024.11.19 |




