<머릿말>

수학은 질서의 학문입니다.
보이지 않는 것을 수학적인 논리에 의해 보이게 합니다.
질서와 아름다운 사회를 위해 공헌한 기호가 있습니다.
많은 기호 중에 으뜸은 바로 화살표 기호입니다.
30여년간 교육현장에서 학생들과 함께한 수학 교실 수업에서 학생들이 왜 어려워하나?
질문을 통해 수학 책을 읽을 수 있게 도와 줘야 겠다는 생각을 하게 되었답니다.
기초가 없다며 선생님 수학은 싫어요, 선생님은 좋아요 라고 말하는 아이들에게
수학도 좋아질 수 있는 방법은 없을까? 수학 책은 왜? 읽을 수 없을까? 어렵게만 표현되어야만 하나?
쉽다고 느껴지는 함수의 개념의 표현을 통해 수학 공부로 힘들어 하는 학생들에게 용기를 주고 싶습니다.
학생들에게 적용했더니 반응이 좋았던 내용을 중심으로 써 내려갑니다.
읽다가 보면 저절로 수학과 친해지는 학습 경험을 하길 기대합니다.
하나님께서는 인간들에게 지혜를 주셨습니다.
이 글을 쓸 수 있도록 도움을 준 딸과 아들 그리고 남편에게 감사하며 이 글을 읽어준 학생들에게 감사를 표합니다.
<글순서>
머릿말
함수의 개념 재 해석(1)_따라가!!!
글을 마치며...
< 함수의 개념 재 해석(1)>_따라가!!!
화살표 기호는 세상에서 방향을 의미합니다.
화살표 표시 본 사람, 자동차 등은 따라가면 목적지까지 안전하게 도착합니다.
세상에서 사랑의 러브라인을 결정할 때도 사용합니다.

러브라인을 짝짓기라고 말합니다.
여성그룹에 {영미, 영순}, 남성그룹에{영철, 영수,영규}가 있습니다.
예를들은 러브라인이 현실화된다면 5명 모두는 행복할 수 있을까? 라는 의심이 듭니다. ㅎ
러브라인을 화살표로 짝짓기를 표현했는데
수학에서 이를 대응이라고 부릅니다.
수학은 명확성을 추구합니다. 짝짓기는 여성그룹과 남성그룹이 있어야 합니다.
수학에서는 여성그룹을 정의역과 남성그룹을 공역이라고 하는 두 집합에서 시작합니다.
정의역에 있는 모든 원소가 공역의 원소에 짝짓기를 대응이라 부릅니다.
여기서 대응하는 방법은 여러가지가 나타납니다.
이 중에서
정의역의 있는 모든 원소가 공역의 원소에
하나씩 빠짐없이 대응시키는 것을 함수라 부릅니다.
수학기호로 나타내면 f : X→ Y 입니다.

수학에서는 정의를 내리고 그림으로 나타낸 것을 수학기호를 사용하여 표현합니다.
다음과 같이 그림을 보고 따라서 3번 반복하여 읽어보고 표현 해 보시길 바랍니다.
스스로 깨닫게 되는 경험할 수 있는 기적이 일어납니다.
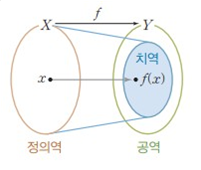
x가 f를 따라가!!! y로 도착 ▶ f(x)=y
첫번째 그림을 보고
영미가 f를 따라가!!! 영규로 도착 ▶ f(영미)=영규
영순이가 f를 따라가!!! 영수로 도착 ▶ f(영순)=영수
이 때, 도착한 것을 수학용어로 함숫값이라고 부릅니다.
영규는 영미의 짝이죠, 수학에서는 영규는 영미의 함숫값이 됩니다.
영수는 영순이에 짝이죠, 수학에서는 영수는 영순이에 함숫값이 됩니다.
여기서
함숫값들의 모임을 치역이라 부릅니다.
교과서적인 표현입니다.


수학은 특수성을 찾아 내고 이름을 붙여 줍니다. 짝짓기 대응 중에 정의역의 각 원소를 하나씩 빠짐없이 대응된 것을 함수라고 정의 했죠. 위 그림 함수 9개 중에서
(7) f(영미)=f(영순)=영철 영미와 영순이 모두 영철이에게 러브라인을 보냈죠.
(8) f(영미)=f(영순)=영수 영미와 영순이 모두 영수에게 러브라인을 보냈죠.
(9) f(영미)=f(영순)=영규 영미와 영순이 모두 영규에게 러브라인을 보냈죠.
(7)(8)(9) 함수는 정의역의 모든 원소(영미, 영순)가 공역의 특정한 값에 모두 대응된 것을 알 수 있습니다.
그래서 (7)(8)(9)는 상수함수라고 이름을 불러주기로 약속했답니다.
(1)~(6)은 영미≠영순(정의역의 영미와 영순이는 같을 수 없죠, 다르죠!)이면 f(영미)≠(영순) 대응 된 것이 달라요.
그래서 (1)~(6)는 일대일함수라고 이름을 불러주기로 약속했답니다.






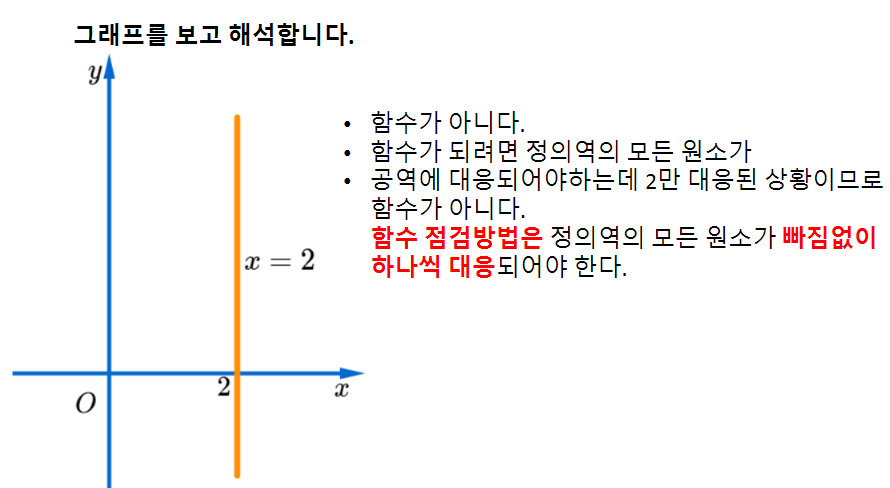

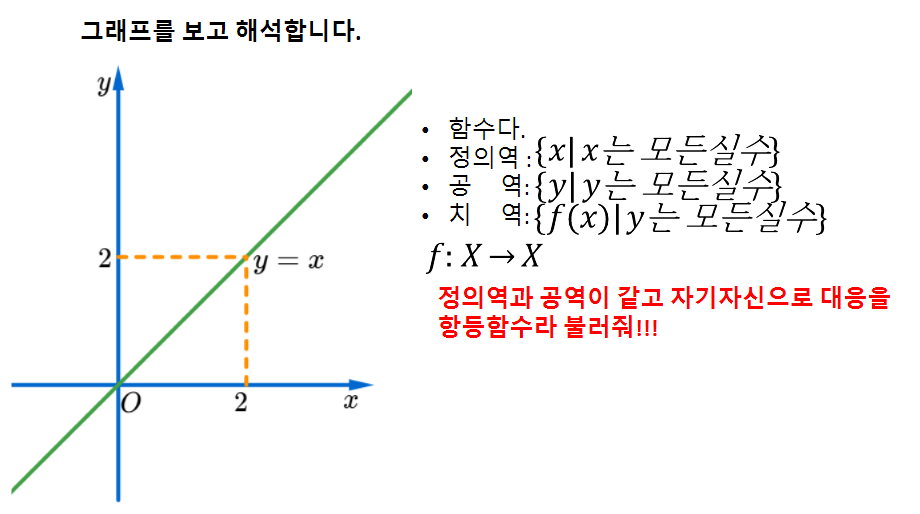
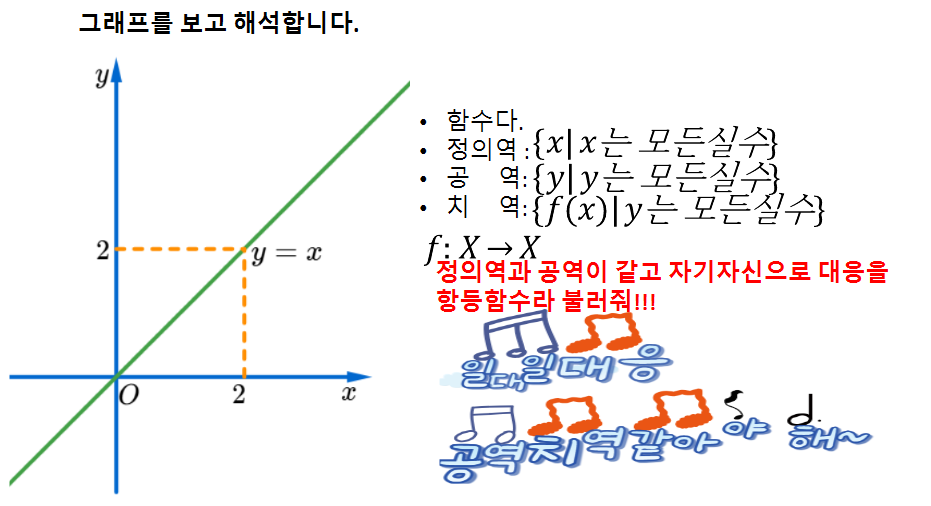







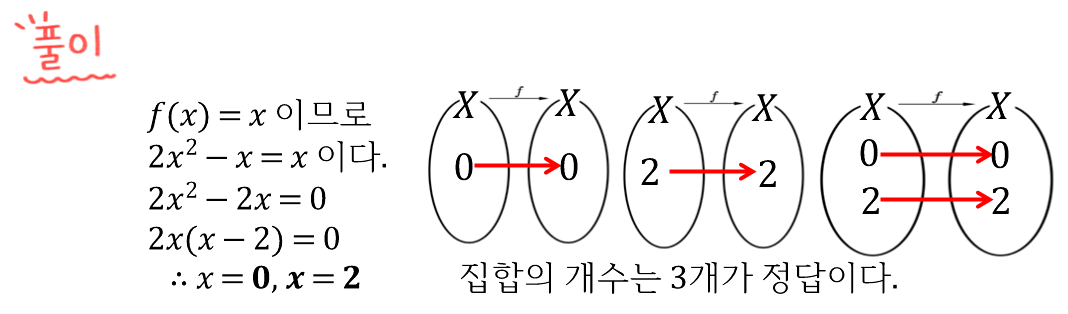
<함수개념의 재해석(1) 글을 마치며...>
지금까지 대응을 출발하여 함수, 일대일함수, 일대일대응, 항등함수, 상수함수, 서로같은함수를 정리해 보았습니다.
이 글을 보고 반복학습을 한다면 좋은 결과를 얻을 수 있고 수학책이 술술 읽히는 경험으로 자신감이 생길겁니다.
하나님은 인간에게 지혜를 주셨습니다.
하나님은 인간에게 진리의 말씀을 주셨습니다.
수학을 통해 하나님을 알 수 있는 기회가 되고 기적을 경험하길바랍니다.


